A note to the reader: For explanation on how to set up the lab environment see the "Introduction" section of the post.
If you're looking for a specific phase:
This phase is definitely the trickiest out of all of the other bomb lab phases. Prepare for data structures…
This phase is a doosey. Let’s go through everything step by step to figure out what we need to do.
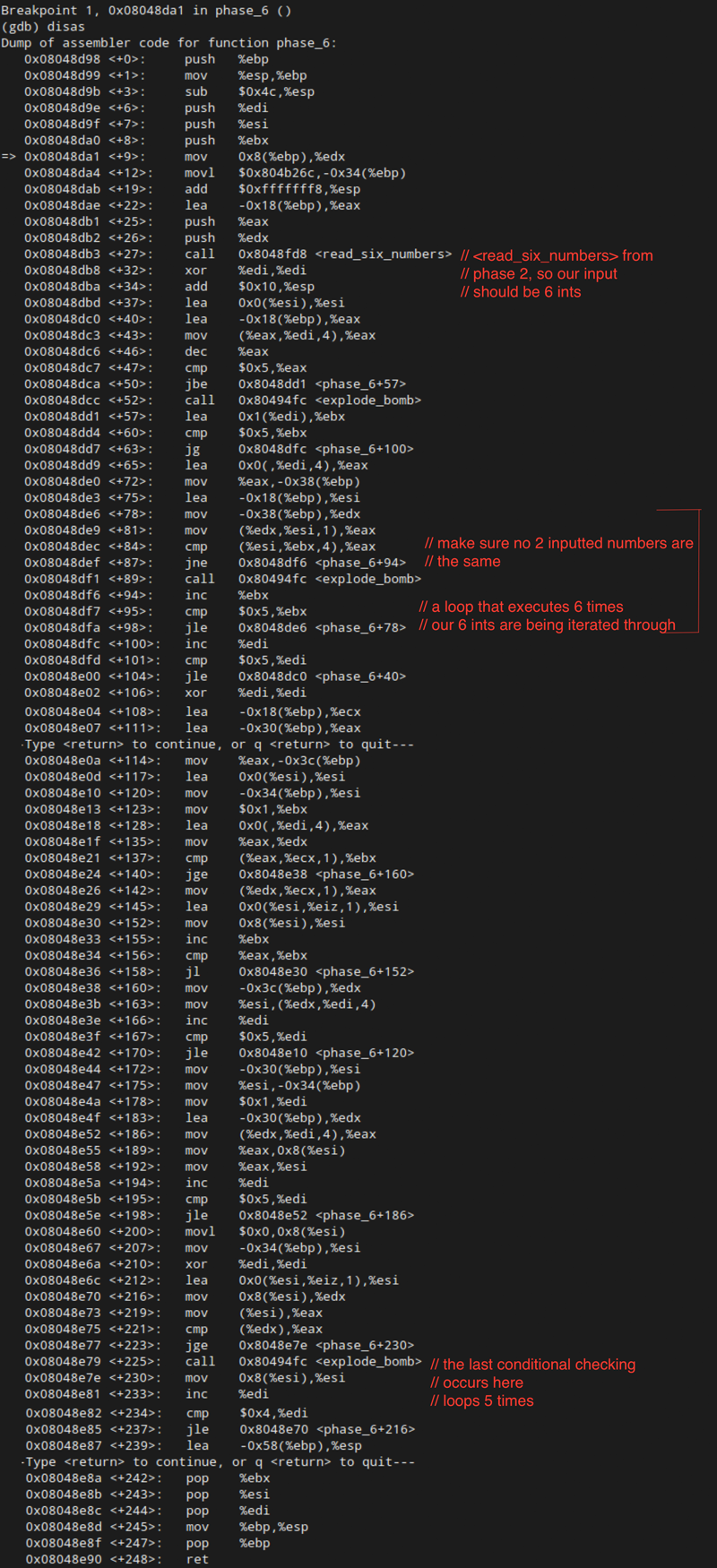
First things first, our friend <read_six_numbers> from Phase 2 is back again. So, our input should be six integers. That one is a gimmie.
Next, we’ve got some loops happening. Firstly, <phase_6+47> is making sure that each number in our password is less than six. Now we have two criteria for our password. It needs to be six integers separated by spaces, and each integer needs to be less than or equal to six.
The final constraint on our input occurs in the nested loops between <phase_6+57> and <phase_6+104>. We have a loop with iterators %ebx and %edi. Essentially what happens is that we compare each number with every other number, and we only jump <explode_bomb> on line <phase_6+89> if the comparisons are not equal. In other words, all six of our integers need to be distinct.
Let’s summarize what we know so far about our input for this phase:
- six integers separated by spaces
- each integer should be less than or equal to 6
- no integer should be the same as any other integer
Now that we have a better idea of what our input should look like, let’s use the test string 1 2 3 4 5 6 and head on down towards the <explode_bomb> call at <phase_6+225> to see if we can find out more.

Here is the conditional statement by itself. First, the contents of %esi + 8 get moved into %edx. Subsequently, %esi itself gets moved into %eax. Then, %eax gets compared to %edx. If the value of %edx (which is %esi + 0x8) is less than the value at %eax (which is %esi) then the bomb explodes.
So, what are these values we’re comparing anyway? Let’s take a look:
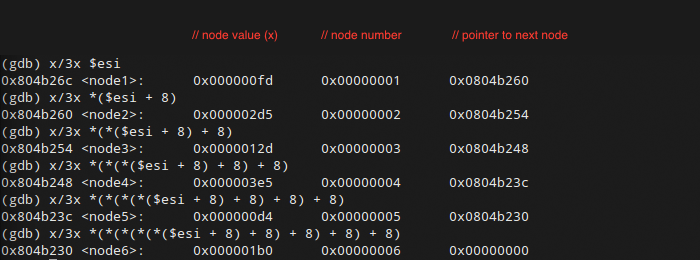
When we take a look at the contents of %esi and %esi + 0x8, we get a couple of structures called <node1> and <node2>. Each node has three elements. The second element here obviously corresponds to the node number itself: 1 for <node1>, 2 for <node2>, etc. The third element of the node looks like a pointer. As we check out the contents of %esi + 0x8, and then ((%esi + 0x8) + 0x8), and so on, we see that these pointers are decreasing 0x8 at a time. Given that the first column of values seem to be arbitrary, this is starting to look like a common data structure: a (singly) linked list. Column one is the value of the node, column two is the node’s position in the list, and column threee is the pointer to the next node in the list.
So now we know, when we compare %edx and %eax at <phase_6+221>, what we’re actually doing is comparing the value of the current linked list node to the value of the next node in the list. If the next node’s value isn’t lower than the present node’s value, the bomb explodes. In other words, we need to put the nodes in order from largest value to smallest value. How do we do this? With our input.
Here’s a table of the values for reference:

And here they are in order from largest to smallest:
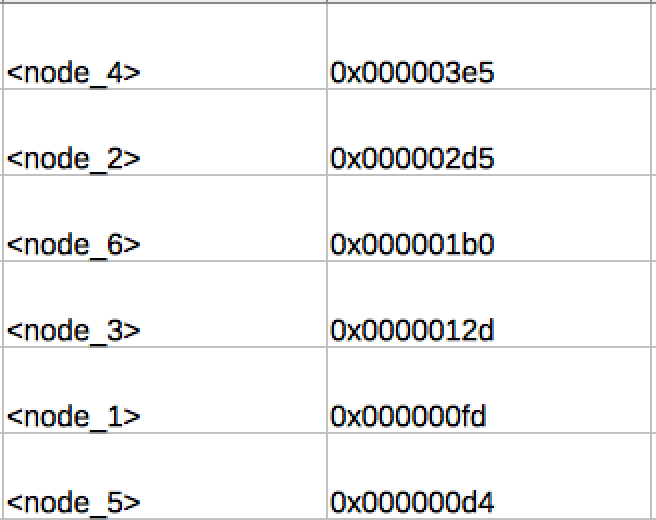
So there you go. That’s the answer right there.
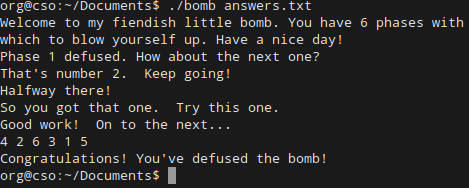
Phase 6 complete! We did it!
Wrap Up
I hope you had fun working through the six levels of the bomb lab with me. I certainly enjoyed it. There’s nothing like quite like some crunchy reverse engineering goodness to get your brain in gear again. For the record, I do know there is a secret phase. While I solved it correctly for my class, I am not going to go through the steps here. If you reallllly need a tutorial, you can find one pretty easily with the search engine of your choice.
Thanks for reading, and I hope you found this tutorial helpful.




